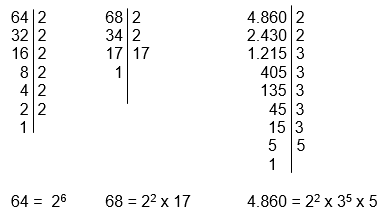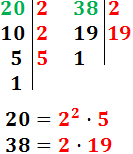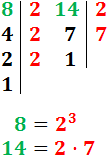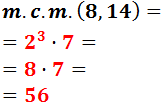Rama de la matemática que trata de la recolección, organización y análisis de datos
con el fin de obtener explicaciones y predicciones sobre fenómenos observados
Algunos conceptos importantes de un estudio estadístico son:
• La población. Es el grupo de elementos o características con propiedades comunes sobre las cuales se dirige un estudio estadístico.
• La muestra. Es un grupo más pequeño tomado de la población pero que permite obtener la misma información. A cada uno de los elementos de la población o la muestra se le denomina individuo.
• Un dato. Es el valor de la variable asociada a un elemento de la población o de la muestra.

• Una variable. Es la característica de interés de cada individuo. Puede ser cualitativa (o de atributos), cuando se refiere a una cualidad de un elemento de la población, o cuantitativa (o numérica), cuando cuantifica un elemento de la población o de la muestra
Distribución de frecuencia: Al resumir grandes colecciones de datos, es útil distribuirlos en clases o categorías y determinar el número de individuos que pertenecen a cada clase llamado frecuencia de clase.
Una disposición tabular de los datos por clases junto con las frecuencias correspondientes de clase se denominan distribuidores de frecuencia o tablas de frecuencia.
Ejemplo
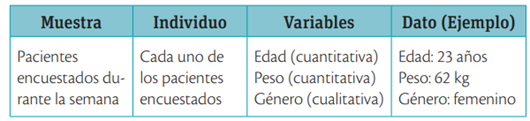
En un centro médico se realizó una encuesta para establecer la edad, el peso y el género de los pacientes atendidos durante una semana.
Especifica los elementos considerados en este estudio estadístico.
Solución: Los elementos de este estudio estadístico se presentan en la Tabla
PRÁCTICA GUIADA
En un instituto educativo con un total de 50 estudiantes, se aplicó a 10 de ellos una prueba de lenguaje sobre 100 puntos, obteniendo los resultados: 53, 53, 53, 54, 55, 70, 75, 75, 85, 90.
Análisis
Población y muestra
Como el total de estudiantes del instituto educativo es 50 estudiantes, entonces la población es 50. Como se aplicó la prueba a 10 estudiantes, entonces la muestra es 10. La calificación en la prueba de lenguaje es la variable.
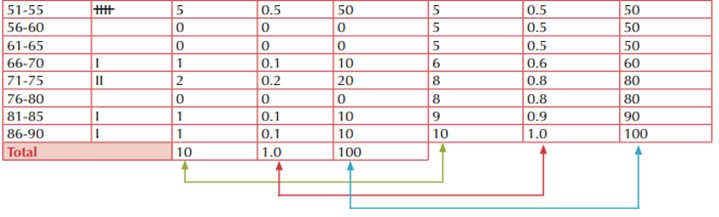
Tabla de frecuencias: Las tablas de frecuencias sirven para condensar o resumir la
información:

Frecuencia Relativa Simple: hi =fi/N
Frecuencia Absoluta Acumulada Fi = Fi = f1 + f2 +…
Frecuencia Relativa Acumulada Hi =h1 + h2 +…
Frecuencia Porcentual Acumulada F% = hi(100)
Frecuencia porcentual simple f % = hi(100)
Gráficas.
La información recopilada puede condensarse o resumirse también en las siguientes gráficas: barras, histograma, polígono de frecuencias o gráfica circular.
Diagrama de barras
Calificación de la prueba de lenguaje

Histograma
Calificación de la prueba de lenguaje

La diferencia entre el diagrama de barras y el histograma es que en el caso de las barras estas tienen un espacio entre ellas, mientras que en el histograma las barras van pegadas.
Polígono de frecuencias
Calificaciones de la prueba de lenguaje

Los segmentos que forman el polígono de frecuencias parten del punto medio de cada una de las barras.
Gráfica circular
Calificaciones de la prueba de lenguaje

Resolver las siguientes situaciones aplicado las conceptualizaciones que vimos anteriormente:
El alcalde de Villavicencio ha decidido invertir en obras sociales para los estratos menos favorecidos y para esto aplicó una encuesta a 50 transeúntes que se encontraban en el parque Santander, para saber que estrato es el que más predomina en el sector. La pregunta que realizo fue: ¿A qué estrato socioeconómico pertenece usted?
La siguiente tabla muestra las respuestas de los 50 encuestados.
a. Determina el tipo de variable que se utiliza en el problema (cualitativa o cuantitativa).
b. Construye la tabla de frecuencias correspondiente.
c. A partir de la tabla de frecuencias, elabora el diagrama de barras correspondiente.
d. ¿Qué nivel socioeconómico tiene una mayor representación?
e. ¿Cuál es el porcentaje de representación de cada estrato?
f. Si la alcaldía decide implementar la obra social en los barrios donde la representación de los
estratos 1 y 2 sea mayor al 67%. ¿Este barrio tendría la inversión de obras sociales?
ESTRUCTURACIÓN-CONCEPTUALIZACIÓN
Medidas en estadística
Mediante las medidas estadísticas logramos resumir la información y conocemos algunos datos importantes que nos permiten emitir conclusiones sobre las poblaciones y hacer comparaciones entre ellas. En los cursos anteriores ya hemos estudiado las medidas de centralización o medidas de tendencia central. El cuadro siguiente muestra una clasificación general de las medidas estadísticas:
PRÁCTICA GUIADA
Medidas de tendencia central
Tomando en cuenta los datos de las calificaciones de la prueba de lenguaje:
53, 53, 53, 54, 55, 70, 75, 75, 85, 90, vamos a identificar la moda, la mediana y la media aritmética o promedio.
Moda (Mo) : La moda (Mo) es el dato que más se repite
53, 53, 53, 54, 55, 70, 75, 75, 85, 90.
. Mo= 53
Mediana (Me): Es el dato que queda en el centro de un conjunto ordenado.
53, 53, 53, 54, 55, 70, 75, 75, 85, 90.
(55+70) ÷ 2 = 62.5
Me = 62.5 que se aproxima a 63 por tener la primera cifra decimal igual o mayor que 5.
Recordemos que cuando el número de datos es impar, la Me es el dato que se encuentra en el centro del conjunto ordenado y cuando el número de datos es par, se promedian los dos datos centrales del conjunto ordenado.
Media aritmética, media, o promedio ( x ): La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
53, 53, 53, 54, 55, 70, 75, 75, 85, 90
Como en 63.3 la cifra decimal es menor que 5, entonces dejamos solamente 63.
ACTIVIDADES PARA DESARROLLAR
Un galpón sacrifica pollos diariamente, para la venta. El número de pollos sacrificados en los últimos 15 días son: 25, 27, 35, 28, 30, 24, 25, 29, 32, 37,30,28, 28, 30,25
Las edades de un grupo de 10 estudiantes de un curso son 15, 17, 15, 18, 10, 14, 15, 19, 12, 17. Encuentra la moda, la mediana y la media aritmética
En un vivero se lleva el registro de las hojas que tienen las plantas en una fecha determinada. Se tomaron ocho plantas al azar y se encontró que el número de hojas que tiene cada una de ellas es: 9, 8, 7, 5, 8, 6, 8, 9. Ordena el conjunto y encuentra las medidas de centralización.
Considera los siguientes datos sobre la concentración de globulina receptora, para una muestra de mujeres con pruebas de laboratorio de evidente anemia por deficiencia de hierro:
Indica la moda, la mediana y la media
El número factorial
n! factorial es el producto de todos los números desde 1 hasta el número dado.
Podemos decir simbólicamente:
n! = 1 x 2 x 3 x 4 … (n 1) (n)
1! = 1
2! = 1 x 2 = 2
3! = 1x 2x 3 = 6
4! = 1x 2 x3 x 4 = 24
5! = 1x 2x 3x 4x 5 = 120
Variaciones
Un arreglo ordenado y sin repetición se denomina variación ordinaria o variación sin repetición. Un arreglo ordenado y con repetición se denomina variación con repetición.
En las variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que: No entran todos los elementos, sí importa el orden y no se repiten los elementos.
PRACTICA GUIADA
Calcular las posibles variaciones de dos elementos que se pueden establecer con las letras m,p y q.
Simbólicamente:
Como m=3 y n= 2, entonces:
Las posibles variaciones de dos elementos que se pueden establecer con las letras m, p y q son seis
Las parejas son: (m,p),(m,q),(p,m),(p,q),(q,m) y (q,p) en este caso las parejas (m,q) y (q,m) son distintas:
Variaciones con repetición Se llama variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que: No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Si importa el orden y se repiten los elementos
Ejemplo: Cuantos números de dos cifras se pueden formar con los dígitos 1,2,3, y 4
Se forman 16 números de dos cifras, veamos cuales son estos números:
11 12 13 14
21 22 23 24
31 32 33 34
41 42 43 44
Permutaciones
Llamamos permutación de un conjunto a cada una de las posibles ordenaciones de todos los elementos de dicho conjunto, de tal forma que: sí entran todos los elementos, sí importa el orden y no se repiten los elementos
Pn = n!
Ejemplo
Dado el conjunto {1, 2, 3}, es posible ordenar sus elementos, sin repetirlos
P3 = 3! = 1 x 2 x 3 Se obtiene 6 permutaciones para estos elementos
{1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2} y {3, 2, 1}
Combinaciones:
Se llama combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos de forma que: no entran todos los elementos, no importa el orden, no se repiten los elementos
Mariana tiene 6 amigas y desea invitarlas a cenar,
pero solo puede invitar a 4 simultáneamente.
¿Cuántos grupos distintos de invitadas puede
tener?
Hay 15 grupos de invitadas a cenar
ACTIVIDADES PARA DESARROLLAR
1. ¿Cuántas palabras se pueden formar con las letras de “FINCA”?
2. ¿Cuántos números de tres cifras pueden formarse con los 4 primeros números pares del conjunto de los números naturales?
3. ¿Cuántos partidos se juegan en un torneo conformado por 6 equipos?
4. ¿De cuántas formas diferentes se pueden cubrir los cargos de presidente, secretario y tesorero de una junta de acción comunal sabiendo que hay 7 posibles candidatos?
5. En la heladería le ofrecen a Martha conos de tres sabores, si la heladería dispone de 5 sabores, ¿Cuántas variaciones de sabores hay?
Experimentos aleatorios y espacio muestral
Algunos de los conceptos que abordaremos, ya son conocidos de los cursos anteriores, y a partir de ellos construirás otros nuevos. Recordaremos aquí lo visto: Piensa en la experiencia aleatoria al hacer los lanzamientos:
a. Una moneda
b. Un dado
La moneda puede caer en cara o en sello y el dado puede caer en uno de los números 1, 2, 3, 4, 5 o 6. A cada uno de estos sucesos se le llama suceso elemental, además, tanto en el caso de la moneda, como en el caso del dado se trata de sucesos equiprobables. Los sucesos equiprobables son aquellos que tienen la misma probabilidad de ocurrir. La probabilidad de ocurrencia la calculamos por la aplicación de la regla de Laplace. Recordemos que para sucesos elementales como los de la moneda o los del dado, la Ley de Laplace, se expresa como:
P (de cada suceso elemental) = 1/ Número de sucesos elementales
Si la moneda no está alterada, la probabilidad de que caiga cara es:
P (cara)=1/2
Caiga cara o cara sello, tienen la misma probabilidad.
Si el dado no está cargado, la probabilidad de que caiga uno
cualquiera de los números de 1 a 6 es siempre igual a 1 /6. Por ejemplo, la probabilidad de que salga 4 es:
P (1) =1/6, es decir, todos los números del dado tienen la misma probabilidad de caer.
Cálculo de probabilidades
Analicemos: ¿Cuál es la probabilidad de todos los sucesos elementales asociados a un experimento? En el caso del lanzamiento de la moneda, hemos visto que hay dos sucesos elementales posibles: cara y sello.
En el lanzamiento de un dado, ¿cuáles son los sucesos elementales posibles? Son seis: sacar 1, sacar 2, sacar 3, sacar 4, sacar 5 y sacar 6. Si el dado es correcto, cada uno de estos sucesos es equiprobable, entonces:
La suma de las probabilidades de todos los sucesos elementales asociados a un experimento aleatorio es 1.
¿Cuál es la probabilidad de no sacar 3? La probabilidad de no sacar 3 es igual a sacar cualquiera de los números menos 3.
La probabilidad de sacar 3 es P (3) =1/6
Como la suma de las probabilidades es 1, entonces, la probabilidad de no sacar 3 es:
Probabilidad de eventos combinados. Regla de la suma:
Veamos la siguiente situación: En una caja se tienen diez tarjetas numeradas del 1 al 10. Se extrae una tarjeta y se quiere determinar:
a. La probabilidad de extraer una tarjeta que tenga el número 4.
b. La probabilidad de sacar el número 9.
c. La probabilidad de elegir al número 4 ó 9.
Solución
El espacio muestral (EM o S) es el conjunto de tarjetas:
EM = S = {2, 3, 4, 5, 6, 7, 8, 9, 10}
El número de elementos del espacio muestral es n (EM) = n(S) = 10.
La regla de Laplace nos dice que la probabilidad de sacar una tarjeta cualquiera es:
La probabilidad de sacar la tarjeta con el número 4 es P (4) = 1/10 porque solo hay una tarjeta con ese número entre 10.
La probabilidad también puede expresarse en forma decimal o en forma porcentual.
Así: P (4) = 1/10 = 0.10 = 0.10×100 = 10%
En c) se pide la probabilidad de que la tarjeta que se extraiga tenga el número 4 o el número 9. Cuando esto sucede, se suman las probabilidades de los eventos ya que «extraer 4» excluye la probabilidad de «extraer 9», esto es:
Esta probabilidad indica que puede suceder uno de los dos eventos mutuamente excluyentes; esto es, que salga la tarjeta con el número 4 o que salga tarjeta con el número 9.
Cuando dos eventos no pueden ocurrir simultáneamente al realizar un experimento, se dice que éstos son mutuamente excluyentes o independientes y para terminar la probabilidad de dos eventos de este tipo se suman las probabilidades de que ocurra cada evento.
ACTIVIDAD PARA DESAROLLAR
2. Si en un juego de dominó se tienen boca abajo las siguientes fichas, determina las cuestiones señaladas.
a. ¿Cuál es la probabilidad de obtener una ficha en la que una de sus partes tenga el número 5?
b. ¿Cuál la de obtener una ficha cuyos números sumen 5?
c. ¿Cuál es la probabilidad de que si una persona toma una ficha ésta sea blanca?
d. Si la primera persona sacó la ficha (5,0), ¿cuál es la probabilidad de que una segunda persona levante una ficha que tenga un 4?
e. ¿Cuál es la probabilidad de que al tomar una ficha tenga el número 6?
i. ¿Cuántos arreglos diferentes se pueden obtener con las 3 últimas fichas? j. ¿Cuál es la probabilidad de que, al tener 5 fichas, la primera persona saque la (5,3) y la segunda la (4,1)?

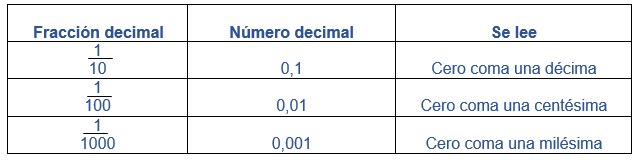
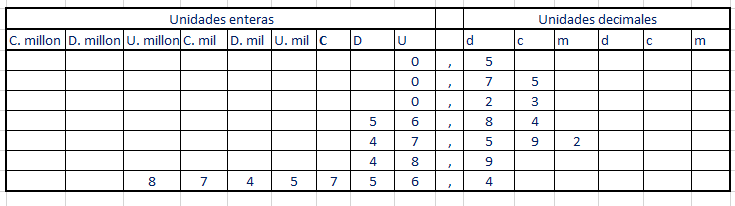
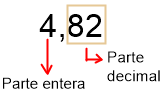 El número 4,82 está formado por 4 unidades, 8 décimas y 2 centécimas
El número 4,82 está formado por 4 unidades, 8 décimas y 2 centécimas

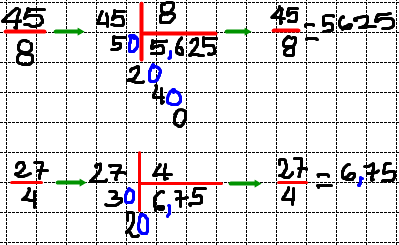 Un número fraccionario se puede escribir en forma decimal, dividiendo el numerador entre el denominador.
Un número fraccionario se puede escribir en forma decimal, dividiendo el numerador entre el denominador.
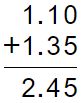 En total necesita 2.45 m. de tela.
En total necesita 2.45 m. de tela.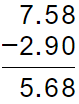












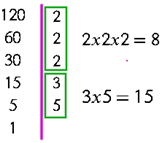




 , donde
, donde  es el radio de la circunferencia.
es el radio de la circunferencia.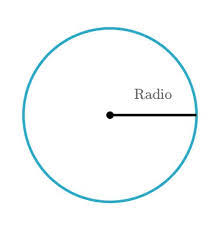


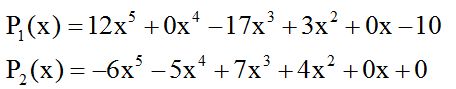
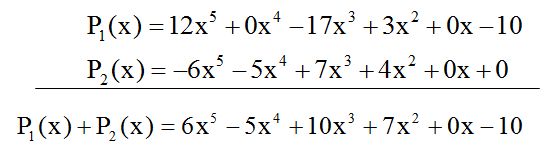
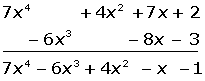







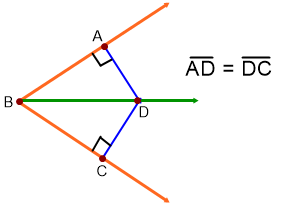

























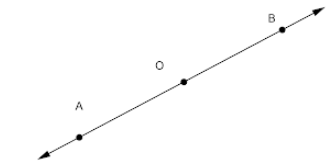

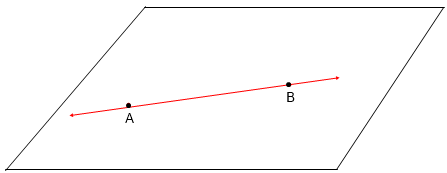


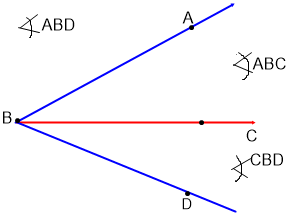
 El punto O es el origen del rayo
El punto O es el origen del rayo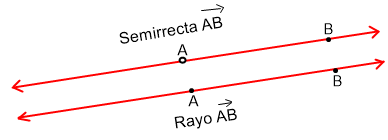
















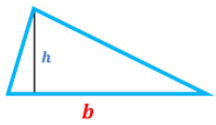
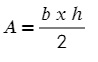 donde b es la base y h la altura
donde b es la base y h la altura
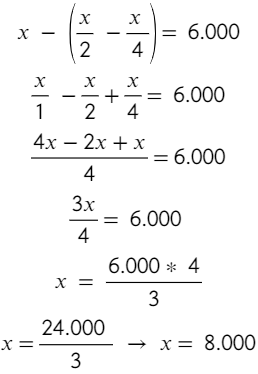



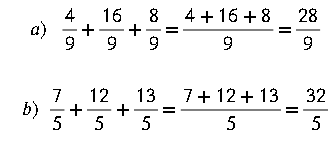





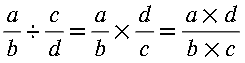





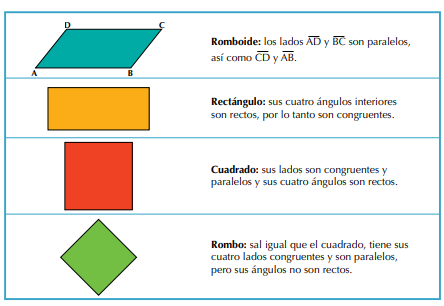
 Como vemos el conjunto A está contenido en el conjunto B
Como vemos el conjunto A está contenido en el conjunto B